Answer:
Approximately
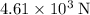 upwards (assuming that
upwards (assuming that
 .)
.)
Step-by-step explanation:
External forces on this astronaut:
- Weight (gravitational attraction) from the earth (downwards,) and
- Normal force from the floor (upwards.)
Let
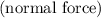 denote the magnitude of the normal force on this astronaut from the floor. Since the direction of the normal force is opposite to the direction of the gravitational attraction, the magnitude of the net force on this astronaut would be:
denote the magnitude of the normal force on this astronaut from the floor. Since the direction of the normal force is opposite to the direction of the gravitational attraction, the magnitude of the net force on this astronaut would be:
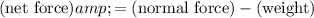 .
.
Let
 denote the mass of this astronaut. The magnitude of the gravitational attraction on this astronaut would be
denote the mass of this astronaut. The magnitude of the gravitational attraction on this astronaut would be
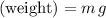 .
.
Let
 denote the acceleration of this astronaut. The magnitude of the net force on this astronaut would be
denote the acceleration of this astronaut. The magnitude of the net force on this astronaut would be
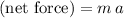 .
.
Rearrange
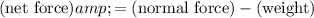 to obtain an expression for the magnitude of the normal force on this astronaut:
to obtain an expression for the magnitude of the normal force on this astronaut:
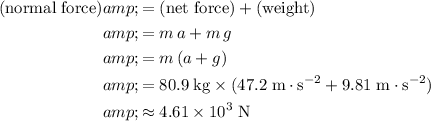 .
.