Question

Help please!!
asap no wrong answers
will give the crown symbol

Answer 1

`\displaystyle 4`

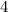
Step-by-step explanation:

`\displaystyle y = Acos(Bx - C) + D`

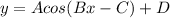
When working with a trigonometric equation like this, always remember the information below:

`\displaystyle Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \\ Wavelength\:[Period] \hookrightarrow (2)/(B)\pi \\ Amplitude \hookrightarrow |A|`

So, the first procedure is to find the period of this graph, and when calculated, you should arrive at this:

`\displaystyle \boxed{(1)/(4)} = (2)/(8\pi)\pi`

You will then plug this into the frequency formula,
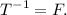`\displaystyle T^(-1) = F.` Look below:

`\displaystyle (1)/(4)^(-1) = F \\ \\ \boxed{4 = F}`

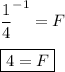
Therefore, the frequency of motion is four hertz.

I am delighted to assist you at any time.

Answer 2

4Hz

Explanation:

Standard form of a sine or cosine function,

y = acos(b(x+c))

where a is the amplitude, b is the value to find the period. and c is the phase shift.

Period = \frac{2\pi}{b}

From the equation given in the question,

`y = 3cos(8\pi \: t + (\pi)/(2) ) \\ y = 3cos(8\pi(t + (1)/(16) )) \: \: (factorising \: 8\pi \: out)`

We can see:

Amplitude = 3,

Period = \frac{2\pi}{8\pi} = 1 / 4

Phase Shift = 1 / 16

Now we want to find the frequency.

Frequency = 1 / Period

= 1 / (1/4)

= 4Hz