Answer: A) 350mL of shampoo and 495 mL of conditioner.
Step-by-step explanation: this problem is solved by a system of two equations, the first one will be the sum of the volumes of the two bottles that equals 845 milliliters:
x+y=845
and the second one will be the sum of the used fractions of shampoo and conditioner, that equals 64 milliliters:

so, for the first equation we have that:
x=845-y
and we substitute this expression into the second equation:
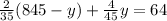
and we solve:
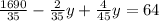
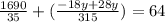
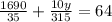
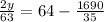
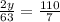
y=495
now with the first equation:
x=845-y
x=845-495
x=350
The shampoo is 350ml and the conditioner is 495ml.