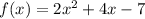Question

(b) Write a quadratic function, in standard form, that fits the set of points. Solve it as a system of three equations, and then check your answers using the TI calculator. Refer to lesson 8.08 p. 314 in your textbook.

(-4, 9), (0, -7), and (1, -1)

Answer 1

`f(x) =2x^(2) +4x-7`

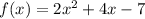
Explanation

Let equation be

`f(x) =ax^(2) +bx+c`

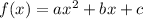
Since (-4,9) satisfy the equation ,plugging x =-4 and f(x) = 9

`f(x) =a(-4)^(2) +b(-4)+c`

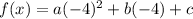
9 = 16a -4b +c ........ equation 1

plugging x =0 and f(x) = -7

-7 = a(0) +b(0) +c

gives c =-7 ......... equation 2

plugging x =1 and f(x) =-1

-1 = a(1) + b(1) +c

-1 = a+b+c ............. equation 3

From equation 2 ,we have c =-7

Plugging this value in equation in 1 and 3 ,we get

16a -4b -7 = 9

16a-4b= 9+7

16a-4b = 16

Dividing the equation by 4 ,we get

4a -b = 4 .......... equation 4

Plugging c =-7 in equation 1 ,we get

a+b+(-7) = -1

a+b = -1+7

a+b = 6 ......... equation5

Adding equation 4 and equation 5

a+b =6

4a-b =4

______________

5a = 10

a = 2

plugging a =2 in equation2

2+b = 6

b = 6-2

b = 4

therefore quadratic equation is

`f(x) =2x^(2) +4x-7`