Question

Let f(x)=2x^2+x-3 and g(x)=x-1. Perform the indicated operation, then find the domain. (F/g)(x)

A. 1/2x+3; domain: all real numbers expect x=-3/2

B. 2x+3;domain: all real numbers

C. 2x^2+3; domain all real numbers

D. 2x+3; domain: all real numbers expect x=1

Answer 1

2x+3; domain: all real numbers expect x=1

The answer is d

Answer 2

The correct option is D.

Explanation:

The given functions are

`f(x)=2x^2+x-3`

`g(x)=x-1`

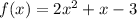
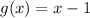
Both functions are polynomial and the domain of any polynomial is the set of all real numbers.

`((f)/(g))x=(f(x))/(g(x))=(2x^2+x-3)/(x-1)`

`((f)/(g))x=(2x^2+3x-2x-3)/(x-1)`

`((f)/(g))x=(x(2x+3)-1(2x+3))/(x-1)`

`((f)/(g))x=((2x+3)(x-1))/(x-1)`

`((f)/(g))x=2x+3`

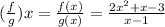
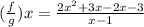
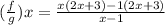
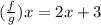
The domain of
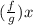`((f)/(g))x` is all real number except x=1, because at x=1, g(x)=0.

Therefore option D is correct.