Answer:
To keep the same volume, the designer needs to decrease the height of the vase by 20%
Explanation:
Volume of cylinder formula is
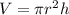
Area of base is
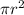 , if this area is increased by 25%, the new area of base would be:
, if this area is increased by 25%, the new area of base would be:
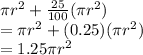
Since volume would be same, we can make the height as:
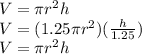
Thus, we can see that the height needs to be divided by 1.25, which we can write in fractional form as:
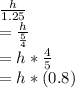
Thus, height needs to be
 of original (or 80% of original)
of original (or 80% of original)