Question

Determine which is the graph of the given function.

Answer 1

The graph of pairwise function is shown below.

Explanation:

The given piece wise function is

`f(x)=\begin{cases}-0.5x+5 & \text{ if } x<1 \\ -0.5(x+5) & \text{ if } x\geq 1 \end{cases}`

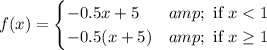
It means for x<1, the function is defined as

`f(x)=-0.5x+5`

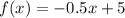
At x=0,

`f(0)=-0.5(0)+5=5`

At x=-1,

`f(-1)=-0.5(-1)+5=5.5`

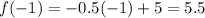
It means the graph passing through (0,5) and (-1,5.5). Joint these point to draw a line of x<1 and there is an open circle at x=1, because the the sign of inequality is <.

It means for x≥1, the function is defined as

`f(x)=-0.5(x+5)`

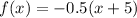
At x=1,

`f(1)=-0.5(1+5)=-3`

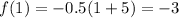
At x=2,

`f(2)=-0.5(2+5)=-3.5`

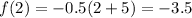
It means the graph passing through (1,-3) and (2,-3.5). Joint these point to draw a line of x≥1 and there is an closed circle at x=1, because the the sign of inequality is ≥.

The graph of pairwise function is shown below.

Answer 2

See attached picture and description below.

Explanation:

Graph each equation as you would graph any linear function. Plot the y-intercept for the first equation at (0,5) then move down 0.5 units and to the right 1 unit. This is the right boundary and should be plotted with an open circle. (red graph.

The second equation should be graphed starting at the y-intercept (0,-2.5) then proceeding down 0.5 units and over 1 unit to the right. (blue graph)

See graph below for complete graph.