Answer:
Option (1), (3) and (6) is correct.
m∠K = 84° , k ≈ 3.7 units and KL ≈ 3.2 units.
Explanation:
Given : ∠J = 58° , ∠L = 38° and length of side JK = 2.3 units.
We need to check all the options and choose that follows.
First we find the measure of ∠K
Using angle sum property , Sum of angles of a triangle is 180°
⇒ ∠J + ∠k + ∠L = 180°
⇒ 58° + ∠k + 38° = 180°
⇒ ∠k + 96° = 180°
⇒ ∠k = 180° - 96°
⇒ ∠k = 84°
Also using sine rule on ΔJKL , we get,

Substitute the values, we get,
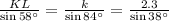
Consider the last two ratios, we have,


On solving we get,
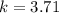
Also, now consider the first and last ratio, we get,
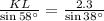
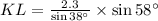
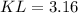
Thus, k ≈ 3.7 units and KL ≈ 3.2 units.
Option (1), (3) and (6) is correct.