Answer:
The sum of even integers between 99 and 301 is 20200.
Explanation:
To find : what is the sum of all the even integers between 99 and 301?
Solution : The even integers between 99 and 301
100 would be least such integer and 300 would be greatest integer
So series form is 100,102,104,106,.......,300
Now applying concepts of an arithmetic progression :
Where, First term, a=100
Common difference,d=102-100=104-102=.....= 2
Last term, l=300
Now the relationship between a,d and I
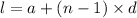
where n is number of terms
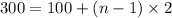
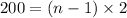
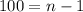
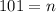
Now we have to find sum of these 101 terms
Sum of n terms of an arithmetic progression is
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2020/formulas/mathematics/high-school/p82o14tt1akmx6szgemiszk1cohd2h7amw.png)
![S_(101)=(101)/(2)[2(100)+(101-1)2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/kt4otmnf8c57rii5mzgusp2s1chq867pfx.png)
![S_(101)=(101)/(2)[200+(100)2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/bjh77s5pq2b12niztbkmsfls8o7v7h6dvi.png)
![S_(101)=(101)/(2)[400]](https://img.qammunity.org/2020/formulas/mathematics/high-school/fwyu8yezz1tje2wc3rnkhwfdx7r1yb37yp.png)
![S_(101)=101*200]](https://img.qammunity.org/2020/formulas/mathematics/high-school/6kkofe02w06jum3kjm97248yjzvsetr7yd.png)
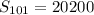
Sum of all even integers between 99 and 301 is 20200.