Answer:
5 and -6
Explanation:
So when a polynomial has zeroes at a, then one of the factors (x-a). This is because in factored form, a polynomial can be written using it's factors as such:
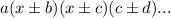 and so on, with the number of factors depending on the degree. The sign is plus or minus because it can be either, it will depend on the sign of the zero. The reason the zeroes are factors, is because when one of the factors is zero it makes the entire thing zero because multiplying them out will always get 0, if you're multiplying by a zero. Anyways, if you have a factor, you can divide, by those factors. So let's do that.
and so on, with the number of factors depending on the degree. The sign is plus or minus because it can be either, it will depend on the sign of the zero. The reason the zeroes are factors, is because when one of the factors is zero it makes the entire thing zero because multiplying them out will always get 0, if you're multiplying by a zero. Anyways, if you have a factor, you can divide, by those factors. So let's do that.
So you have the two factors (x+2)(x-2). So let's divide by each factor. In this example I'll be using long division. So essentially what long division, is finding how many times the leading coefficient of the dividend (x^4+x^3-34x^2-4x+120) can be divided by the leading coefficient of the divisor ((x-2)(x+2)). And then whatever you get, that will be part of the quotient, then take whatever you got, and multiply it by the divisor and then subtract that product from the dividend and then continue this process until the dividend is equal to 0 or you can't divide any further./
Original equation:
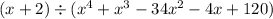
Divide the leading coefficients:

The x^3 will be part of the quotient, now multiply this by the divisor
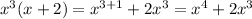
Subtract the product from the dividend
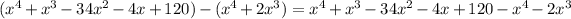
Group like terms:
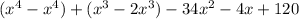
Simplify:
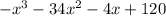
Divide leading coefficients:
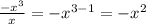
The -x^2 will be part of the quotient, now multiply this by the divisor:
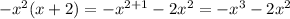
Subtract this from the dividend:
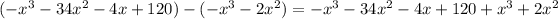
Group like terms:
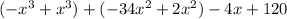
Simplify:
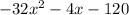
Divide the leading coefficients:
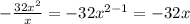
This will be part of the quotient, now multiply this by the divisor:
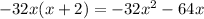
Subtract this from the dividend
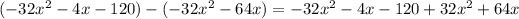
Group like terms:
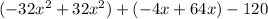
Simplify:
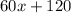
Divide the leading coefficients:
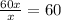
This will be part of the quotient, multiply it by the divisor:
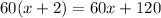
Subtract this from the dividend:
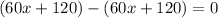
Since this comes out perfectly to zero there is no remainder, and this is expected since it's a factor. You now take all the quotients from dividing the leading terms and you get
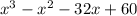 . To keep the original equation you simply multiply it, and you get:
. To keep the original equation you simply multiply it, and you get:
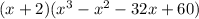 . But what we really care about is the x^3-x^2-32x+60. We now divide it by the other factor x-2 using the same process
. But what we really care about is the x^3-x^2-32x+60. We now divide it by the other factor x-2 using the same process
Original equation:
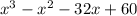
Divide leading terms:
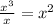
This will be part of the quotient, multiply it by the divisor
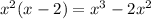
Subtract this from the dividend
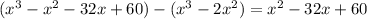
Dividing leading coefficients:
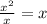
This will be part of the quotient, multiply it by the divisor:
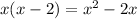
Subtract this from the dividend:
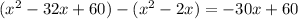
Divide the leading terms:
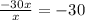
This will be part of the quotient, now multiply it by the divisor:
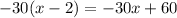
Subtract it from the dividend:
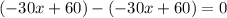
Now take all the quotients of the leading terms and you get:
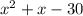
Now we can factor this quadratic to get the equation in completely factored form: We're looking for factors that multiply to -30 and add to 1. So we really need to look for factors that have a difference of 1, Or in other words |a-b| = 1. The sign can be determined after we fine the two factors. The factors 5 and 6 have a difference of 1, and since it needs to add to 1, the 5 has to be negative, and the 6 has to be positive.
So we get the factors:
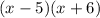 . Setting each of them equal to zero gets you:
. Setting each of them equal to zero gets you:
x-5 = 0
x = 5
x + 6 = 0
x = -6
So the other two zeroes are 5 and -6