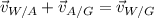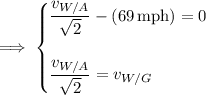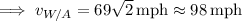Question

The nine ring wraiths want to fly from barad-dur to rivendell. rivendell is directly north of barad-dur. the dark tower reports that the wind is coming from the west at 69 miles per hour. in order to travel in a straight line, the ring wraiths decide to head northwest. at what speed should they fly (omit units)?

Answer 1

Velocity of the ring wraiths relative to the air:

`\vec v_(W/A)=(v_(W/A)\cos45^\circ,v_(W/A)\sin45^\circ)=\left((v_(W/A))/(\sqrt2),(v_(W/A))/(\sqrt2)\right)`

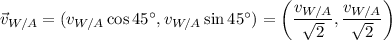
The speed
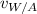`v_(W/A)` is what we want to find - this is the speed at which the wraiths are flying in the air.

(Note:
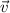`\vec v` denotes velocity, while
`v` denotes speed)

Velocity of air relative to the ground:

`\vec v_(A/G)=((69\,\mathrm{mph})\cos180^\circ,(69\,\mathrm{mph})\sin180^\circ)=(-69,0)\,\mathrm{mph}`

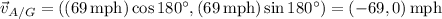
The ring wraiths want their trajectory to be due north, which means their velocity relative to the ground should be

`\vec v_(W/G)=(v_(W/G)\cos90^\circ,v_(W/G)\sin90^\circ)=(0,v_(W/G))`

To an observer on the ground,
`v_(W/G)` is the speed at which the wraiths would appear to be moving in the air.

The relative velocities satisify

`\vec v_(W/A)+\vec v_(A/G)=\vec v_(W/G)`

`\implies\begin{cases}(v_(W/A))/(\sqrt2)-(69\,\mathrm{mph})=0\\\\(v_(W/A))/(\sqrt2)=v_(W/G)\end{cases}`

`\implies v_(W/A)=69\sqrt2\,\mathrm{mph}\approx98\,\mathrm{mph}`