Answer:
Option (a) is correct.
Vertex: (2,36); zeros: (–4,0), (8,0) y-intercept: (0,32)
Explanation:
Consider the given equation

We have to find vertex, zero(s), and y-intercept.
First we find the vertex, For The general form of a quadratic is

the coordinate of the vertex (h, k) is given as
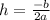 and
and
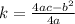
Here, a= -1 , b= 4 and c = 32
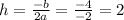 and,
and,
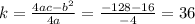
Thus vertex of
 is ( 2, 36)
is ( 2, 36)
Now, we find the zeros,
Put y = 0, we get,
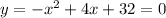
This is a quadratic equation of the form

Hence, we can find zero using middle term splitting method,
4x can be written as 8x - 4x
Thus,


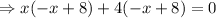
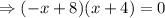
 or
or
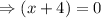
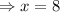 or
or
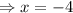
Thus, zeros are (-4,0) and (8,0) .
Now to calculate y intercept put x = 0 in

We get , y= 32.
The same can be seen through graph as below.
Thus, option (a) is correct.