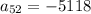Answer:
Common difference(d)
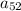
(21) -10 -548
(22) -7 -323
(23) 10 547
(24) -100 -5118
Explanation:
Let the common difference be denoted by 'd'.
Also the nth difference of an arithmetic sequence is given by:
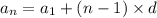
(21)
We are given a recursive formula as:
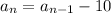
The first term is given by:
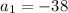
The common difference for an arithmetic sequence is given by:
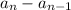
Hence, here we have the common difference as:
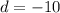
The nth term of an arithmetic sequence is given by:
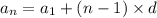
Here
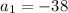 and
and
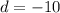 .
.
Hence,
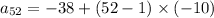
Hence,
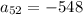
(22)
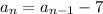
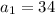
The common difference for an arithmetic sequence is given by:
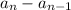
Hence, here we have the common difference as:

Here
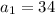 and
and
 .
.
Hence,
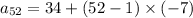
Hence,
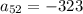
(23)


The common difference for an arithmetic sequence is given by:
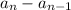
Hence, here we have the common difference as:
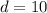
Here
 and
and
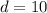 .
.
Hence,
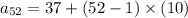
Hence,
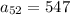
(24)
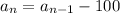

The common difference for an arithmetic sequence is given by:
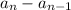
Hence, here we have the common difference as:

Here
 and
and
 .
.
Hence,
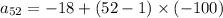
Hence,