Solution:
Consider, the Cubic polynomial :
f(x)=
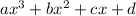
Draw , the graph of cubic polynomial on two dimensional coordinate plane, and find number of times it cuts the x axis.The point where it cuts the x axis,are the roots of the cubic polynomial function or number of real roots that a cubic polynomial function possess is number of times it cuts the x axis.
Keep in mind, Imaginary root occur in pairs.
So, a cubic polynomial function has all real root , a single real root or no real root.
So, if graph cuts the x axis at three points (Either same or different) , showing the number of real roots possessed by the cubic polynomial function.