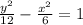Answer:
D.
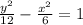
Explanation:
we are given
we can use standard equation of hyperbola
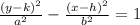
where
center=(h,k)
center at origin
so, h=0 and k=0
vertex is
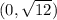
we can use formula
vertices: (h, k + a)
we get
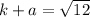
we can plug k=0
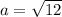
now, we can plug these values
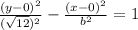
now, we are given it passes through
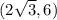
so, we have
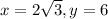
we can plug these values and then we can solve for b
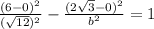
and we get
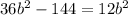
we can solve for b
and we get
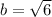
now, we can plug these values
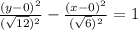
we can simplify it
and we get