Question

Which of the following is a point slope equation of a line that passes through the points (10,5) and (4,-7)?

Answer 1

B) y - 5 = 2(x - 10)

Explanation:

Slop = (5+7)/(10-4) = 12/6 = 2

Point slope form:

y - 5 = 2(x - 10)

or

y + 7 = 2(x - 4)

Answer 2

For this case we have that the point slope equation of a line is given by:

`y-y_ {0} = m (x-x_ {0})`

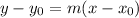
Where "m" is the slope and
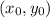`(x_ {0}, y_ {0})` is a point belonging to the line.

Then, we find the slope, for this we need two points:

`(x_ {1}, y_ {1}) = (10,5)\\(x_ {2}, y_ {2}) = (4, -7)\\m = \frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}\\m = \frac {-7-5} {4-10}\\m = \frac {-12} {- 6}\\m = 2`

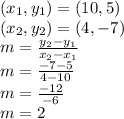
We build the equation by choosing any of the points:

`y-5 = 2 (x-10)`

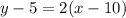
Answer:

`y-5 = 2 (x-10)`

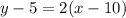
Option B