Answer:
A.
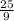
Explanation:
We have been given that Cube A and Cube B are similar solids. The volume of cube A is 27 cubic inches, and the volume of cube B is 125 cubic inches. We are asked to find the the number of times the base area of cube b is larger than the base area of cube A.
We know that volume of cube with each side of
 units is equal to
units is equal to
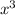 .
.
First of all, we will find the each side of cube A and B as:
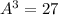
![\sqrt[3]{A^3} =\sqrt[3]{27}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hupdycegy2dwzlk35ju3tbnx48ntslb0h5.png)

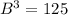
![\sqrt[3]{B^3} =\sqrt[3]{125}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/idj1bbfoklkgoqifltinyl8hh9iuvurozs.png)
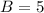
Now, we will find base area of both cubes as:

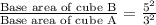

Therefore, the base area of cube B is
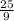 times larger than the base area of cube A.
times larger than the base area of cube A.