Question

Suppose you wanted to make a buffer of exactly ph 7.00 using kh2po4 and na2hpo4. if the final solution was 0.10 m in kh2po4, what concentration of na2hpo4 would you need? (pka for h3po4, h2po−4, and hpo2−4 are 2.14, 6.86, and 12.40, respectively.)

Answer 1

Answer:- 0.138 M

Solution:- The buffer pH is calculated using Handerson equation:

`pH=pKa+log((base)/(acid))`

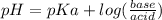
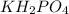`KH_2PO_4` acts as a weak acid and
`Na_2HPO_4` as a base which is pretty conjugate base of the weak acid we have.

The acid hase two protons(hydrogen) where as the base has only one proton. So, we could write the equation as:

`H_2PO_4^-\rightleftharpoons H^++HPO_4^-^2`

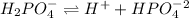
Phosphoric acid gives protons in three steps. So, the above equation is the second step as the acid has only two protons and the base has one proton.

So, we will use the second pKa value. The acid concentration is given as 0.10 M and we are asked to calculate the concentration of the base to make a buffer of exactly pH 7.00.

Let's plug in the values in the equation:

`7.00=6.86+log((base)/(0.10))`

`7.00-6.86=log((base)/(0.10))`

`0.14=log((base)/(0.10))`

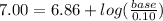
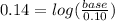
Taking antilog:

`10^0^.^1^4=(base)/(0.10)`

`1.38=(base)/(0.10)`

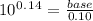
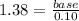
On cross multiply:

[base] = 1.38(0.10)

[base] = 0.138

So, the concentration of the base that is
`Na_2HPO_4` required to make the buffer is 0.138M.