Question

A spinner for a board game consists of a cardboard circle with two plastic arrows anchored to its center. The arrows are congruent isosceles triangles connected at their bases, as shown. Heron’s formula: Area = The base of each triangle measures 2 centimeters and the perimeter of each triangle is 10 centimeters. What is the approximate total area of the plastic triangles on the spinner? 3.9 square centimeters 6.7 square centimeters 7.7 square centimeters 13.4 square centimeters

Answer 1

Option (c) is correct.

The approximate total area of the plastic triangles on the spinner is 2 × 3.9 square centimeters = 7.7 square centimeters

Explanation:

Given:A spinner for a board game consists of a cardboard circle with two plastic arrows anchored to its center. The arrows are congruent isosceles triangles connected at their bases.

also, Given: The base of each triangle measures 2 centimeters and the perimeter of each triangle is 10 centimeters.

We have to find the approximate total area of the plastic triangles on the spinner.

Perimeter of triangle is the sum of sides.

Since given the triangle to be isosceles .

Let the two equal side be x cm, then,

Perimeter of given triangle = 1 0

⇒ x + x + 2 = 1 0

⇒ 2x = 8

⇒ x = 4

Thus, side of triangle is 4 cm.

Now we find the area of isosceles triangle.

We first find the height, using Pythagoras theorem,

`(AC)^2=(AD)^2+(DC)^2`

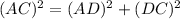
Putting values, we get,

`(4)^2=(AD)^2+(1)^2`

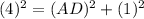
Solving we get,

`AD=3.87`

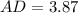
Thus, area of one isosceles triangle
`A=(1)/(2) bh`

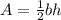
area of one isosceles triangle
`A=(1)/(2) * 2 * 3.87`

On solving we get,

Approximate area of one plastic triangles on the spinner is 3.9 square centimeters.

Thus, the approximate total area of the plastic triangles on the spinner is 2 × 3.9 square centimeters = 7.7 square centimeters

Option (c) is correct.