Answer:
(c)
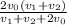
Step-by-step explanation:
Average speed is calculated as (total distance)/(total time). We have three segments in the journey, indexed by 0, 1, and 2:
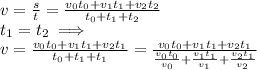
We also know that the distance of the first segment is the same as one of segment 2 and 3 together:

Going back to the average speed expression, divide by t_1:
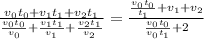
and combine the two equations:
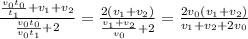
The last form matches your choice (c).