Question

What is the length of XPY in terms of pie?

A) 30 pi m
B) 10 pi m
C) 300 pi m
D) 100 pi m

Answer 1

The correct option is A.

Explanation:

Given information: The radius of the circle is 20m and central angle of arc XY is 90 degrees.

The central angle of arc XPY is

`\text{Central angle of arc XPY}=360-90`

`\text{Central angle of arc XPY}=270`

Multiply this angle by
`(\pi)/(180)`, to convert is into radian.

`\text{Central angle of arc XPY}=270* (\pi)/(180)`

`\text{Central angle of arc XPY}=(3\pi)/(2)`

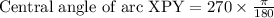
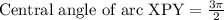
The formula for arc length is

`l=r\theta`

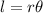
Where, r is radius and θ is central angle in radian.

`l=20* (3\pi)/(2)`

`l=30\pi`

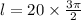
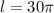
The length of XPY in terms of pie is 30π m. Therefore the correct option is A.

Answer 2

A

Explanation:

The angle subtended at the centre of the circle by arc XPY is 270°

That is 360° - 90° = 270°

arc length = circumference × fraction of circle

= 2πr ×
`(270)/(360)`

= 2π × 20 ×
`(3)/(4)`

= 40π ×
`(3)/(4)` = 30π m → A