Answer:
a) The equation in intercept form by factoring is (x+6)(x+4)
b) From the given graph x- intercepts are (-4,0) and (-6,0) and zeros (roots) of the function are -6 and -4.
c) The solutions of
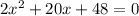 is
is
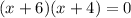 that is x= -6 and x = -4.
that is x= -6 and x = -4.
Explanation:
The given quadratic equation is

Put the function f(x) = 0 , then
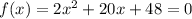
a) The equation in intercept form by factoring is ,
Consider the given function,
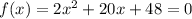
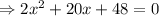
taking 2 common, we get,
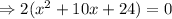
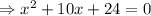
The above is a quadratic equation of the form

Solving quadratic equation using middle term splitting method,
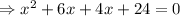
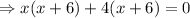
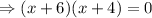
Thus, The equation in intercept form by factoring is (x+6)(x+4).
b) From the given graph x- intercepts are (-4,0) and (-6,0) .
Zeroes / roots of a function are those points where the value of the function is zero.
Put f(x) = 0 as solved above
that is
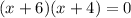
 or
or
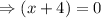
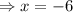 or
or
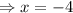
Thus, zeros (roots) of the function are -6 and -4.
For checking put x = -6 and -4 in the function we get f(x) =0 .
c) The solutions of
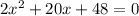 is
is
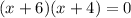 that is x= -6 and x = -4 as shown above.
that is x= -6 and x = -4 as shown above.