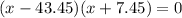Answer:
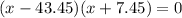
Explanation:
We have the quadratic equation
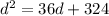 i.e.
i.e.
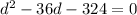
As, the roots of the quadratic equation
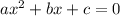 are given by
are given by
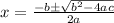 .
.
So, from the given equation, we have,
a = 1, b = -36 , c = -324.
Substituting the values in
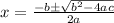 , we get,
, we get,
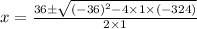
i.e.
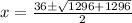
i.e.
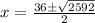
i.e.
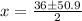
i.e.
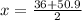 and
and
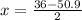
i.e.
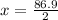 and
and
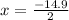
i.e. x = 43.45 and x = -7.45
Thus, the roots of the equation are 43.45 and -7.45.
Hence, the factored form of the given expression will be