Question

In 2012, the population of a city was 6.93 million. The exponential growth rate was 2.18% per year.

a) Find the exponential growth function.
b) Estimate the population of the city in 2018.
e) When will the population of the city be 10 million?
d) Find the doubling time.

Answer 1

`\textsf{a)} \quad f(x)=6.93(1.0218)^x`

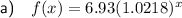
b) 7.89 million (2 d.p.)

c) 2019

d) 32.14 years (2 d.p.) after 2012

Explanation:

Exponential Function

`y=ab^x`

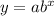
where:

• a is the initial value (y-intercept)
• b is the base (growth/decay factor) in decimal form
• x is the independent variable
• y is the dependent variable

If b > 1 then it is an increasing function

If 0 < b < 1 then it is a decreasing function

Part (a)

If the exponential growth rate was 2.18% per year, then each year there would be 102.18% of the previous year's population.

⇒ b = 1.0218

Given:

• a = 6.93 million
• b = 1.0218
• x = time (in years after 2012)
• y = population (in millions)

Substitute the given values into the formula to create an exponential growth function:

`f(x)=6.93(1.0218)^x`

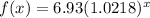
Part (b)

To estimate the population of the city in 2018, determine the value of x:
`x = 2018 - 2012 = 6`

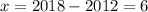
Substitute the found value of x into the found exponential function:

`\implies f(6)=6.93(1.0218)^6=7.89 \: \sf million\:(2\:d.p.)`

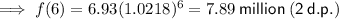
Part (c)

To determine when the population of the city will be 10 million, set the function to 10 and solve for x:

`\implies 6.93(1.0218)^x=10`

`\implies (1.0218)^x=(10)/(6.93)`

`\implies \ln (1.0218)^x= \ln \left((10)/(6.93)\right)`

`\implies x\ln (1.0218)= \ln \left((10)/(6.93)\right)`

`\implies x= (\ln \left((10)/(6.93)\right))/(\ln (1.0218))`

`\implies x=17.00496413...`

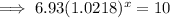
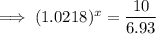
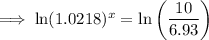
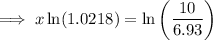
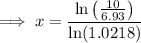
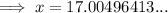
To find the year, add the found value of x to 2012:

`\implies \sf 2012 + 17.00496413... = 2019`

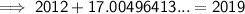
Part (d)

To find the doubling time, set the function to double the initial population and solve for x:

`\implies 6.93(1.0218)^x=6.93 \cdot 2`

`\implies (1.0218)^x=2`

`\implies \ln (1.0218)^x= \ln (2)`

`\implies x \ln (1.0218)= \ln (2)`

`\implies x = (\ln (2))/(\ln (1.0218))`

`\implies x=32.14107014...`

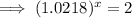
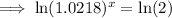
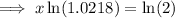
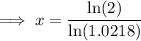
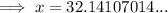
Therefore, the doubling time is 32.14 years (2 d.p.) after 2012.

Answer 2

Given

• Initial population of a city - 6.93 million people,
• Growth rate - 2.18% per year.

To find

• a) The exponential growth function,
• b) Population of the city in 2018,
• e) Time when population is 10 million,
• d) The doubling time for population.

Solution

a) The growth function has the form:

• 
  `P(x) = P*(1 + r)^x`,

where:

• P(x) - population after x years,
• P- initial population,
• r - rate of change,
• x - number of years since 2012.

Considering the values we get the function:

• 
  `P(x) = 6.93*(1 + 2.18/100 ) ^x=6.93*1.0218^x`

b) Number of years between 2012 and 2018 is:

• x = 2018 - 2012 = 6

Find the population, using the above equation:

• 
  `P(6) = 6.93*1.0218^6 = 7.89` million (rounded)

c) Find the value of x when P(x) = 10 million

• 
  `10 = 6.93*1.0218^x`
• 
  `1.0218^x = 10/6.93`
• 
  `1.0218^x=1.443`
• 
  `log1.0218^x=log1.443`
• 
  `x = log1.443/log1.0218`
• 
  `x=17` years

d) Find the doubling time:

• 
  `2*6.93 =6.93*1.0218^x`
• 
  `1.0218^x=2`
• 
  `x=log2/log1.0218`
• 
  `x=32.14` years