Answer:
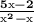 (choice D)
(choice D)
You have the correct answer.
=====================================================
Work Shown:
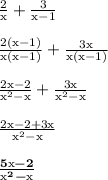
--------
Step-by-step explanation:
The idea I used is that we cannot add the fractions unless the denominators are the same. The denominators x and (x-1) lead to the lowest common denominator, aka LCD, of
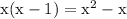 . We multiply the denominators together to get the LCD.
. We multiply the denominators together to get the LCD.
The first original fraction
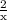 is missing (x-1) in the denominator. This is why I multiplied top and bottom by (x-1) in the 2nd step. Similarly, the fraction
is missing (x-1) in the denominator. This is why I multiplied top and bottom by (x-1) in the 2nd step. Similarly, the fraction
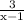 is missing an x out front to get to x(x-1). This is why I multiplied top and bottom of that fraction by x.
is missing an x out front to get to x(x-1). This is why I multiplied top and bottom of that fraction by x.
After we get the denominators to be the same, we can then add the numerators like any other algebraic expression. The denominator stays the same the entire time.
It's similar to how
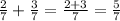 has the numerators add like you'd expect while the denominator stays at 7 the entire time.
has the numerators add like you'd expect while the denominator stays at 7 the entire time.
You can think of it like this: "2 sevenths + 3 sevenths = 5 sevenths" or "2s+3s = 5s" for short. The term "sevenths" is effectively a unit such as cm or meters. We must have common units if we want to add them.