Answer:
Given the inequality:
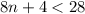
Subtract 4 from both sides we have;
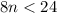
Divide 8 to both sides we have;
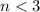
The solution set for this inequality is:
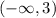
Let any 3 values from this solution sets:
n = 2
then;
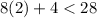
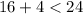
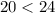 true
true
Similarly for:
n = 1
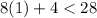
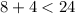
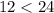 true
true
For n =0
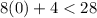
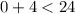
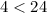 true
true
Therefore, the 3 values that would make this inequality true
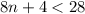 is, {0, 1, 2}
is, {0, 1, 2}