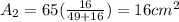Answer: 49 cm² and 16 cm²
Explanation:
1. If the triangles are similar and the ratio of the perimeter os 4:7, then the areas are in the following ratio:
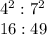
2. You know that the sum of their areas is 65 cm², then, you can calculate the area of the larger triangle as following:
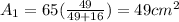
3. The area of the smaller triangle is: