Question

A,B and C are the vertices of one triangle.

A has a coordinate of (4,6)
B has a coordinate of (2,-2)
C has a coordinate of (-2,-4)

D is the midpoint of AB
E is the midpoint of AC

Prove that DE is parallel to BC
You must show each stage of your working out.

Answer 1

Explanation:

If DE and BC are parallel, then they have the same slope.

We have

A(4, 6), B(2, -2), C(-2, -4)

The formula of a midpoint:

`\left((x_1+x_2)/(2),\ (y_1+y_2)/(2)\right)`

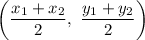
D is the midpoint of AB, and E is a midpoint of AC.

Calculate the coordinateso fo D and E:

`D\left((4+2)/(2),\ (6+(-2))/(2)\right)\to D\left((6)/(2),\ (4)/(2)\right)\to D(3,\ 2)\\\\E\left((4+(-2))/(2),\ (6+(-4))/(2)\right)\to E\left((2)/(2),\ (2)/(2)\right)\to E(1,\ 1)`

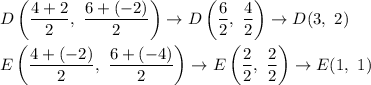
The formula of a slope:

`m=(y_2-y_1)/(x_2-x_1)`

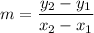
Calculate the formula of a DE and BC:

`DE:\\\\m_(DE)=(2-1)/(3-1)=(1)/(2)\\\\BC:\\\\m_(BC)=(-4-(-2))/(-2-2)=(-4+2)/(-4)=(-2)/(-4)=(1)/(2)`

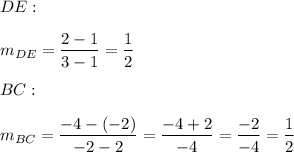
The slope DE and the slope BC are the same.

Therefore DE is parallel to BC.

Answer 2

Explanation:

Given: The triangle with coordinate A(4,6), B(2,-2) and C(-2,-4). D is the mid point of AB and E is the mid point of AC.

To prove: DE is parallel to BC.

Construction: Join DE.

Proof: If we prove the basic proportionality theorem that is
`(AD)/(DB)=(AE)/(EC)`, then it proves that DE is parallel to BC.

Now, Mid Point D has coordinates=
`((4+2)/(2),(6-2)/(2))=(3,2)` and Mid Point E has coordinates=
`((4-2)/(2),(6-4)/(2))=(1,1)`

Now, AD=
`\sqrt{(4-3)^(2)+(6-2)^(2)}=√(17)`

DB=
`\sqrt{(3-2)^(2)+(2+2)^(2)}=√(17)`

AE=
`\sqrt{(4-1)^(2)+(6-1)^(2)}=√(34)`

EC=
`\sqrt{(1+2)^(2)+(1+4)^(2)}=√(34)`

Now,
`(AD)/(DB)=(AE)/(EC)`

=
`(√(17))/(√(17))=(√(34))/(√(34))=(1)/(1)`

Hence,
`(AD)/(DB)=(AE)/(EC)`

Thus, By basic proportionality theorem, DE is parallel to BC.