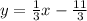Answer:
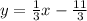
Explanation:
We are given the line x-3y=3.
We want to write the equation of the line that is parallel to this line, and that passes through (2, -3).
Parallel lines have the same slope.
Therefore, let's find the slope of x-3y=3.
The line is currently written in standard form, which is ax+by=c, where a, b, and c are free integer coefficients.
In order to find the slope of this line, we can convert it into slope-intercept form, which is y=mx+b, where m is the slope and b is the value of y at the y intercept.
To do that, we need to isolate y on one side; this is the same as solving the equation for y.
x - 3y = 3
Start by subtracting x from both sides
-3y = -x + 3
Now divide both sides by -3
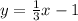
The slope of the line is 1/3, as 1/3 is the coefficient in front of x.
It is also the slope of our new line.
Since the question doesn't specify which format for the equation of the line, we can use any form. However, let's put the equation of the new line into slope-intercept form.
So, substitute 1/3 as m in y=mx+b.
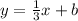
Now we need to find b.
As the equation passes through the point (2, -3), we can use its values to help solve for b.
Substitute 2 as x and -3 as y.
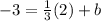
Multiply.
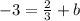
Subtract 2/3 from both sides (we can write this as an improper fraction).
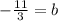
Substitute -11/3 as b in the equation.