Question

The length of a side of a triangle is 36. A line parallel to that side divides the triangle into two parts of equal area. Find the length of the segment determined by the points of intersection between the line and the other two sides of the triangle. WHOEVER SEES THIS PLEASE HELP ME ASAP!

Answer 1

Length of DE is : 18√2 units

Explanation:

The length of a side of a triangle is 36.

To calculate : The length of the segment DE

Now, the two parts of triangle have equal area ∴ Area(ADE) = Area(BDEC)

`\implies Area(ADE)=(1)/(2)* Area(ABC) \\\\\implies (Ar(ADE))/(Ar(ABC))=(1)/(2)`

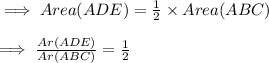
In ΔABE and ΔABC,

∠A = ∠A (Common angles)

∠ABE = ∠ABC (Corresponding angles are always equal)

By AA postulate of similarity of triangles, ΔABE ~ ΔABC.

Hence by area side proportionality theorem

`(Ar(ADE))/(Ar(ABC))=((DE)/(BC))^2\\\\\implies (1)/(2)=(DE^2)/(36^2)\\\\\implies DE^2=(36^2)/(2)\\\\\bf\implies DE=18√(2)\textbf{ units}`

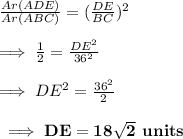
Hence, length of DE is 18√2 units