Question

A set of data has a normal distribution with a mean of 50 and a standard deviation of 6. What percent of the data should be less than 50?

Answer 1

The percent of the data should be less than 50 is 50%

Explanation:

we are given

mean=50

`\mu=50`

standard deviation is 6

`\sigma=6`

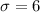
and

x=50

so, we can use formula

`z=(x-\mu)/(\sigma)`

now, we can plug values

`z=(50-50)/(6)`

`z=0`

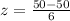
Since, the data should be less than 50

so,

`z<0`

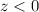
now, we can use normal distribution table

we get

`P(z<0)=0.50`

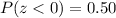
So,

The percent of the data should be less than 50 is 50%