Answer:
The function's formula is
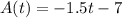 .
.
Explanation:
It is given that Mr. Mole left his burrow that lies 7 meters below the ground and after 6 minutes, he was 16 meters below the ground.
It means the line passing thought the points (0,-7) and (6,-16). It means the initial value is -7.
He started digging his way deeper into the ground, descending at a constant rate. The rate of change is

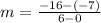
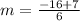
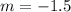
The rate of change is -1.5.
A(t) denote Mr. Mole's altitude relative to the ground A (measured in meters) as a function of time t (measured in minutes).
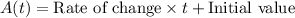
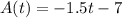
Therefore the function's formula is
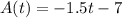 , here negative sign shows the Mr. Mole's altitude relative to below the ground A.
, here negative sign shows the Mr. Mole's altitude relative to below the ground A.