Question

The volume of construction work was increased by 60% but the productivity of labor increased by only 25%. By what percent must the number of workers be increased in order for the work to be completed in time, as it was scheduled originally?

Answer 1

Answer: The answer is 28%.

Step-by-step explanation: Given that the volume of construction work was increased by 60% and the productivity of labour increased by 25% only. We are to find the percentage by which the number of workers must increase to complete the in time.

Let 'V' be the volume of construction work, 'p' be the productivity of labour, 'n' be the number of workers, and 'x' be the percentage by which the number of workers must increase.

According to the question, we have

`V=r* n,\\\\(8)/(5)V=(5)/(4)r* n(1+x).`

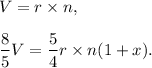
Dividing the second equation by the first equation, we have

`((8)/(5)V)/(V)=((5)/(4)nr(1+x))/(nr)\\\\\Rightarrow (8)/(5)=(5)/(4)(1+x)\\\\\Rightarrow 1+x=(32)/(25)\\\\\Rightarrow x=(7)/(25)=0.28.`.

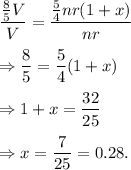Thus, the required percentage of workers that must increase in order to complete the work in time as scheduled originally is 28%.