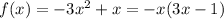Answer:
Hence, the quadratic equation is:
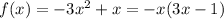
Explanation:
Let the quadratic formula be given by:
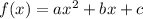
Now we are given the interpolating points and there corresponding values as:
(-1,-4), (0,0) and (2,-10).
this means then x=-1 f(x)=-4
when x=0 then f(x)=0
and when x=2 then f(x)=-10
so we first put x=0
then f(x)=0=c
hence c=0.
now we are left with the function:

Hence now we put x=-1 in equation (1)
we get:
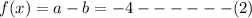
now we put x=2
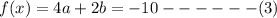
On solving equation (2) and (3) by elimination we get:
Multiply equation (2) by 2 and add to equation (3) we obtain;
2a-2b= -8
4a+2b= -10
---------------------------
6a=-18
⇒ a= -3 on dividing both side by 6.
Hence on putting the value of a in equation (2) we get:
b=1
Hence, the quadratic equation is: