Question

Since BC is parallel to DE, triangles ABC and ADE are similar. What are the lengths of the unknown sides? It would be a great help

Answer 1

Answer: AC= 10 cm and CE= 5 cm

Explanation:

In the given picture, Δ ADE is a right triangle

∴ By Pythagoras theorem,

`AD^2+DE^2=AE^2\\\Rightarrow\ (8+4)^2+9^2=AE^2\\\Rightarrow\ AE^2=12^2+9^2\\\Rightarrow\ AE^2=144+81=225\\\Rightarrow\ AE=15\ cm`

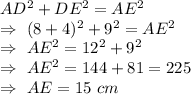
Since triangles ABC and ADE are similar and corresponding sides of similar triangles are proportional therefore,

`(AB)/(AC)=(AD)/(AE)\\\Rightarrow(8)/(AC)=(12)/(15)\\\Rightarrow\ AC=(8*15)/(12)\\\Rightarrow\ AC=10\ cm`

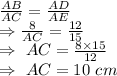
Now, AE=AC+CE

⇒CE=AE-AC

⇒CE=15-10=5 cm