Question

You invest $5,000 into an account where interest compounds continuously at 3.5%. How long will it take your money to double? Round answer to nearest year.

Answer 1

20 years

Explanation:

Continuous Compounding Formula

`\large \text{$ \sf A=Pe^(rt) $}`

where:

• A = Final amount
• P = Principal amount
• e = Euler's number (constant)
• r = annual interest rate (in decimal form)
• t = time (in years)

Given:

• A = $10,000
• P = $5,000
• r = 3.5% = 0.035

Substitute the given values into the formula and solve for t:

`\sf \implies 10000=5000e^(0.035t)`

`\sf \implies (10000)/(5000)=e^(0.035t)`

`\sf \implies 2=e^(0.035t)`

`\sf \implies \ln 2=\ln e^(0.035t)`

`\sf \implies \ln 2=0.035t\ln e`

`\sf \implies \ln 2=0.035t(1)`

`\sf \implies \ln 2=0.035t`

`\sf \implies t=(\ln 2)/(0.035)`

`\implies \sf t=19.80420516...`

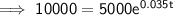
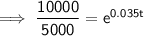
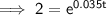
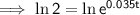
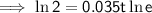
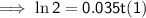
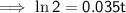
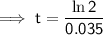
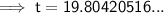
Therefore, it will take 20 years (to the nearest year) for the initial investment to double.