Question

In parallelogram DEFG, DH = x + 1, HF = 3y, G H = 3 x − 4 , and HE = 5y + 1. Find the values of x and y. The diagram is not drawn to scale.

Answer 1

Answer: The value of x and y is 5 and 2 respectively.

Explanation:

Since we know that "Diagonals of parallelogram bisects each other":

So, we have given that

in parallelogram DEFG,

DH = x + 1, HF = 3y, G H = 3 x − 4 , and HE = 5y + 1.

so, According to question, as shown in the figure below:

`DH=HF\\\\x+1=3y\\\\x-3y=-1-----------(1)`

Similarly,

`GH=HE\\\\3x-4=5y+1\\\\3x-5y=1+4\\\\3x-5y=5----------------(2)`

Using Substitution Method to solve system of equation:

From eq(1), we get

`x=-1+3y`

Putting the value of x in eq (2), we get

`3x-5y=5\\\\3(-1+3y)-5y=5\\\\-3+9y-5y=5\\\\4y=5+3\\\\4y=8\\\\y=(8)/(4)\\\\y=2`

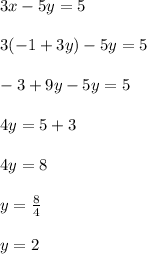
Now,, put the value of y to get the value of x:

`x=-1+3y\\\\x=-1+3(2)\\\\x=-1+6\\\\x=5`

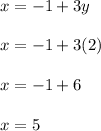
Hence, the value of x and y is 5 and 2 respectively.