Question

What's the vertex and axis of symmetry of y= -2x^2 + 8x-20

Answer 1

Vertex

V = (2, -12)

Axis of symmetry

x = 2

Explanation:

To answer this question suppose the general equation of a parabola of the form:

`ax^2 + bx + c`

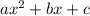
Where a, b and c are constants that belong to real numbers.

So it is known that the vertex of this parable is:

`x = (-b)/(2a)`

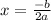
So, we use this same formula to find the vertex of the parabola
`y = -2x^2 + 8x-20`

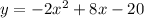
Where:

`a = -2\\b = 8\\c = -20\\\\x = (-b)/(2a)\\\\x = (-8)/(2 (-2))\\\\x = 2`

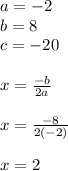
The vertex of the parabola is at the point

V = (2, -12)

Finally, the axis of symmetry of a parabola always passes through its vertex. Then the axis of symmetry is the straight line

x = 2