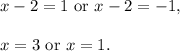Question

Complete each statement in the steps to solve x2 – 4x + 3 = 0 using the process of completing the square. Isolate the constant by ________ both sides of the equation. Add ____ to both sides of x2 – 4x = –3 to form a perfect square trinomial while keeping the equation balanced. Write the trinomial _____ x2 – 4x + 4 as squared. Use the square root property of equality to get x – 2 = ± _____ . Isolate the variable to get solutions of 1 and 3.

Answer 1

2022 answer

Explanation:

Answer 2

1. Add -3

2. Add 4

3. Write the trinomial as
`(x-2)^2`

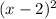
4.
`\pm 1`

Explanation:

1. Isolate the constant from the equation
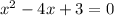`x^2-4x+3=0` by adding -3 to both sides of the equation. Then

`x^2-4x+3+(-3)=0+(-3),\\ \\x^2-4x=-3.`

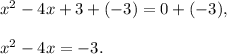
2. Add 4 to both sides of equation
`x^2-4x=-3:`

`x^2-4x+4=-3+4,\\ \\x^2-4x+4=1.`

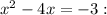
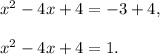
3. Write the trinomial
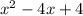`x^2-4x+4` as perfect square:

`x^2-4x+4=(x-2)^2.`

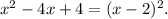
4. Use the square root property to get

`x-2=1\text{ or }x-2=-1,\\ \\x=3\text{ or }x=1.`