Question

What is a quadrict function with only the two real zeros given x = -4 and x= -1

Answer 1

`y=x^4+5x^3+5x^2+5x+4`

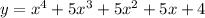
Explanation:

Quadratic function is the function whose degree is 2.

`f(x)=ax^2+bx+c`

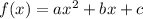
We have been given two zeroes of the quadratic function:

We will put values of x in the function. The function where we will get zero is the quadratic function.

Option 4 is the quadratic function.

Put x=-4 in
`y=x^4+5x^3+5x^2+5x+4`

`\Rightarrow y=(-4)^4+5(-4)^3+5(-4)^2+5(-4)+4`

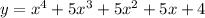
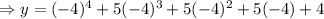
On simplification we get:

`y=0`

Now, put x=-1 in
`y=x^4+5x^3+5x^2+5x+4`

`y=(-1)^4+5(-1)^3+5(-1)^2+5(-1)+4`

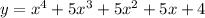
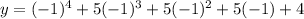
On simplification we get:

`y=0`