Question

((Picture) CONVERGENT AND DIVERGENT SERIES PLEASE HELP!!

Answer 1

This series is convergent

(A)

Explanation:

We are given a series

Firstly, we will find nth term

So, numerator is

`=2n+1`

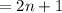
So, denominator is

`=n!`

so, nth term will be

`a_n=(2n+1)/(n!)`

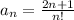
now, we can use ratio test

`L= \lim_(n \to \infty) (a_n_+_1)/(a_n)`

`L= \lim_(n \to \infty) ((2n+3)/((n+1)!))/((2n+1)/(n!))`

`L= \lim_(n \to \infty) (2n+3)/(\left(n+1\right)\left(2n+1\right))`

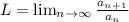
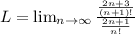
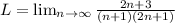
Since, denominator has two n terms

so, we get

`L=0<1`

So, this series is convergent