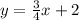Question

here's a graph of a linear function. write the equation that describes that function. express it in slope intercept form. HELP!

Answer 1

`y=(3)/(4)x+2`

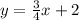
Explanation:

So when you express a linear function in slope-intercept form it's given in the form of y=mx+b, where m is the slope, and b is the y-intercept. This is because as x increases by 1, the y-value will increase by m (because multiplication), and since the slope is defined as rise/run, the rise will be m, and run will be 1, giving you a slope of m/1 or m. The reason b is the y-intercept, is because whenever the linear function crosses the y-axis, the x-value will always be 0. Meaning that mx will be 0 because m * 0 will equal 0... and that leaves b by it self, so b will determine the y-intercept.

So if you look at the graph, the linear function crosses the y-axis as (0, 2) so the value of b will be 2. This gives you the equation y=mx+2.

Now to calculate the slope, we can take any two points and see how much the rise was and how much the run was. It can also be more formally defined in the equation:
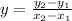`y=(y_2-y_1)/(x_2-x_1)`. So let's take the points (0, 2) and (8, 8). As you can see the x-value increases by 8 or "ran" by 8, and the y-value increased by 6. So the rise over run in this case is 6/8 which can simplified as 3/4. That is the slope. This gives you the complete equation of:
`y=(3)/(4)x+2`