Answer:
Option (3) is correct.
The given expression
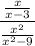 is equivalent to
is equivalent to
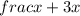
Explanation:
Given expression
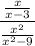
We have to find an equivalent fraction to the given expression
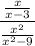 out of given options.
out of given options.
Consider the given expression
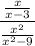
Divide fractions
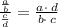
We have,
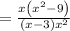
Cancelling common factor x, we have

Using algebraic identity
 , we have,
, we have,
Apply on
 we get,
we get,
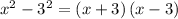
Substitute, we get,
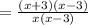
Cancelling out common factor (x-3) , we get
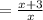
Thus, the given expression
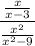 is equivalent to
is equivalent to
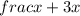
Option (3) is correct.