Question

A boat is heading towards a lighthouse, whose beacon-light is 148 feet above

the water. The boat's crew measures the angle of elevation to the beacon, 8°.
What is the ship's horizontal distance from the lighthouse (and the shore)?
Round your answer to the nearest hundredth of a foot if necessary.
Answer:
feet
Submit Answer
attempt 1 out of 2 / problem 2 out of max 4

Answer 1

x = 1053.07 ft

Explanation:

So if you look at the diagram I drew it might become a bit more apparent what you have to do. For this problem you'll need to use one of the six trigonometric functions. In this case you know the angle and the opposite side of the angle, and you need the adjacent side. The trigonometric function tan is defined as
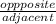`(oppposite)/(adjacent)`. So let's plug in the known values:

`tan(8) = (148)/(x)`

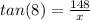
multiply both sides by x

`tan(8) * x = 148`

Divide both sides by tan(8)

`x=(148)/(tan(8))`

Calculating tan of 8 degrees using a calculator

`x=(148)/(0.141)`

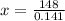
Simplify

x = 1053.07 ft