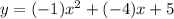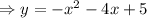Question

Find an equation in standard form of the parabola that passes through (-2, 9), (-4, 5), and (1, 0)

Answer 1

We know the parabolic function:

`y=ax^2+bx+c`

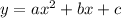
We will use the points to form the equation (-2,9) we will get:

`9=a(-2)^2+b(-2)+c`

`9=4a-2b+c`

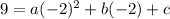
Now, using (-4,5) we will get:

`5=16a-4b+c`

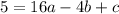
Now, using (1,0) we will get:

`0=a+b+c`

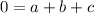
Now, using these three equations we will find a,b and c

On solving equations: a=-1,b=-4 and c=5

Now, using a,b and c in the general equation we get:

`y=(-1)x^2+(-4)x+5`

`\Rightarrow y=-x^2-4x+5`