Question

if a equals 8, 2 b equals 11, 13 and C equals 2, 6 classify the following triangle as either right or isosceles

Answer 1

isosceles

Explanation:

I took the quiz and got the question correct. I promise isosceles is the correct answer.

Answer 2

Triangle is isosceles

Explanation:

Isosceles triangle is a triangle in which two sides are equal. To identify the above triangle as isosceles or right we need to find the length of sides.

The length of line as shown in figure can be calculated for points A(x1,y1) and B(x2,y2) as:

length of a line=
`√((x2-x1)^2+(y2-y1)^2)`

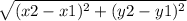
As shown in figure of triangle, the three points are A(8,2), B(11,13) and C(2,6)

Length of AB=
`√((x2-x1)^2+(y2-y1)^2)`

=
`√((11-8)^2+(13-2)^2)`

=
`√((3)^2+(11)^2)`

=
`√(130)`

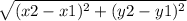
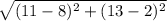
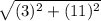
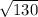
Length of AC=
`√((x2-x1)^2+(y2-y1)^2)`

=
`√((8-2)^2+(2-6)^2)`

=
`√((6)^2+(-4)^2)`

=
`√(52)`

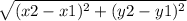
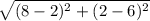
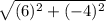
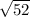
Length of BC=
`√((x2-x1)^2+(y2-y1)^2)`

=
`√((11-2)^2+(13-6)^2)`

=
`√((9)^2+(7)^2)`

=
`√(130)`

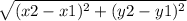
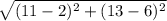
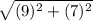
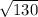
AB=BC [As stated in condition above, two sides are same or equal ]

Therefore, we can see that the triangle is isosceles.