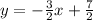Question

Which is the equation in slope-intercept form for the line that passes through (−1, 5) and is parallel to 3x + 2y = 4?

y=−23x+72

y=−32x+72

y=32x−72

y=23x+72

Answer 1

`y=-(3)/(2)x+(7)/(2)`

Explanation:

So when two lines are parallel there slopes are the same, but there y-intercepts are different, since if they had the same y-intercept, then they would be the same exact line. To convert an equation into slope-intercept form you simple isolate y by moving everything else to the other side, and then divide by the coefficient of y so the coefficient of y becomes 1. This will give you the equation in the form: y=mx+b where m is the slope and b is the y-intercept (because when the linear equation crosses the y-axis, the x is 0, thus mx will be 0, leaving only b, so the y-intercept is b).

Original Equation:

3x + 2y = 4

Subtract 3x from both sides

2y = -3x + 4

Divide both sides by 2

y = -3/2x + 2

Generally any parallel line will be in the form:

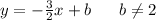`y=-(3)/(2)x + b\ \ \ \ \ b\\e2`. Since as stated before if two lines have the same slope and y-intercept, they're the same line, which is not the same as parallel, since parallel lines never intersect.

So since we're given a point in the parallel line (-1, 5) we can plug those values into the equation to find the value of b

`5=-(3)/(2)(-1) + b`

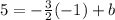
Multiply and

`5=(3)/(2)+ b`

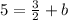
Convert 5 into a fraction with a denominator of 2

`(5)/(1) * (2)/(2) = (10)/(2)`

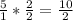
Write equation using this form of 5:

`(10)/(2)=(3)/(2)+b`

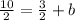
Subtract 3/2 from both sides

`(7)/(2)=b`

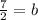
Now take this value and input it into the slope-intercept form to finish the equation:
`y=-(3)/(2)x+(7)/(2)`