Question

Help with this please

Answer 1

Yes, the given parallelogram is a rectangle.

Explanation:

The vertices of parallelogram are J(-5,0), K(1,4), L(3,1) and M(-3,-3).

The slope formula is

`m=(y_2-y_1)/(x_2-x_1)`

`JK=(4-0)/(1-(-5))=(4)/(6)=(2)/(3)`

`KL=(1-4)/(3-1)=(-3)/(2)`

`LM=(-3-1)/(-3-3)=(-4)/(-6)=(2)/(3)`

`JM=(-3-0)/(-3-(-5))=(-3)/(2)`

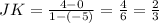
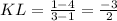
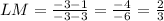
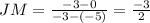
The slopes of opposites sides are same it means they are parallel to each other.

The product of slopes of two consecutive sides is

`(2)/(3)* (-3)/(2)=-1`

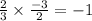
Since the product of slopes of two consecutive sides is -1, therefore the consecutive sides are perpendicular to each other.

Yes, the given parallelogram is a rectangle.