Question

The figures shows the show the dimension of a tennis court and a basketball court given in term of the width x in feet of the tennis court.

TENNIS. X.

2X+6.



BASKETBALL. 1/2X+32

3X-14







A: write an expression for the perimeter of each court:


B: write an expression that describe how much greatwr the perimeter of the basketball court is than the perimeter of the tennis court:


C: suppose the tennis court is 36feet wide. Find all dimensions of the two courts

Answer 1

The basketball court is old

Explanation:

Answer 2

A. 6X+12 and 7X+36 respectively

B. X+24

C. Dimensions are 36 feet × 78 feet and 50 feet × 94 feet respectively

Explanation:

We are given,

Dimensions of the perimeter court is X and 2X+6.

Dimensions of the basketball court is
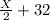`(X)/(2)+32` and 3X-14.

Since, both the courts are similar to a rectangular base.

Moreover, the perimeter of a rectangle = 2(L+W)

Thus, perimeter of the tennis court = 2(X+2X+6) = 2(3X+6) = 6X+12

And, perimeter of the basketball court =
`2[((X)/(2)+32)+(3X-14)]` =
`2[3X+(X)/(2)+32-14]` =
`2[(7X)/(2)+18]` = 7X+36

So, the perimeters of tennis and basketball court are 6X+12 and 7X+36 respectively.

Now, Perimeter of Basketball Court - Perimeter of Tennis court = 7X+36 - 6X+12 = X + 24

Hence, the perimeter of basketball court is bigger than the tennis court by X+24

Further, the width of the tennis court is 36 feet i.e. X = 36.

So, length of the perimeter = 2X+6 = 2×36 + 6 = 78 feet.

Thus, dimensions of the tennis court are 36 feet × 78 feet.

Moreover, the dimensions of the basketball court are
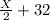`(X)/(2)+32` = tex]\frac{36}{2}+32[/tex] = 18+32 = 50 feet and 3X-14 = 3×36-14 = 108-14 = 94 feet.

Thus, dimensions of the basketball court are 50 feet × 94 feet.