Question

The area of a rectangle is 45 cm2. Two squares are constructed such that two adjacent sides of the rectangle are each also the side of one of the squares. The combined area of the two squares is 106 cm². Find the lengths of the sides of the squares.

Answer 1

Answer: 5 cm and 9 cm

Explanation:

If the two squares are x and y, then

xy = 45

x^2 + y^2 = 106

so,

x^2 + (45/x)^2 = 106

x^2 + 2025/x^2 = 106

x^4 - 106x^2 + 2025 = 0

(x^2-25)(x^2-81) = 0

x^2 = 25 and 81

x = 5 and 9

yep, 5*9 = 45

Answer 2

The lengths of sides of squares are 5 cm and 9 cm.

Explanation:

Let the sides of rectangle be x and y .

Area of rectangle = Length × Breadth

Given : Area of rectangle = 45 cm².

⇒ x × y = 45

⇒
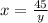`x=(45)/(y)` ........(1)

Two squares are constructed such that two adjacent sides of the rectangle

so squares have side x and y .

Area of square = side × side

Area of square with side x = x²

Area of square with side y = y²

Also, The combined area of the two squares is 106 cm².

⇒ x² + y² = 106

From (1) put value of x , we get,

`((45)/(y))^2+y^2=106`

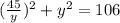
Solving for y ,

`((45)/(y))^2+y^2=106`

`2025+y^4=106y^2`

`y^4-106y^2+2025=0`

`y^4-81y^2-25y^2+2025=0`

`y^2(y^2-81)-25(y^2-81)=0`

`(y^2-25)(y^2-81)=0`

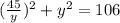
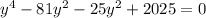
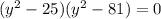
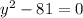`y^2-81=0` or
`y^2-25=0`

on solving we get y = 5 and y = 9

Also, x can be find by putting in (1),

⇒
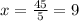`x=(45)/(5)=9` and ⇒
`x=(45)/(9)=5`

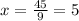
⇒ x = 9 and x = 5

Thus, lengths of sides of squares are 5 cm and 9 cm.